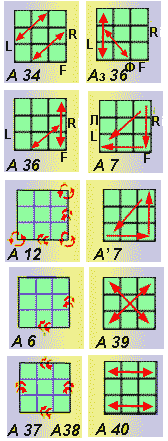
Process (A36) rearranges two next onboard cubes and one is temporary for angular to the scheme, not changing color of a side.
R(U*2) - R'U' - R(U*2)L' - UR'U'L ......A36
The same action makes mirror process A3_36
L'(U*2)LU - L'(U*2)RU' - LUR'...........A3_36
For a turn of onboard and angular cubes of last side the algorithm is sometimes good. A' 12 - clockwise and (A12) against.
FU(F*2) - LF(L*2) - UL(U*2)..............A12
(U*2)L'U' - (L*2)F'L' - (F*2)U'F'........A' 12
If process to do twice angular cubes will be developed only. The sign on a turn thus will change on return. for a turn at once two next onboard cubes it is possible to use algorithm A6.
(R*2)(F*2) - (R*2)(F*2) - RU'(R*2)U - FRU(F*2) - U'F.....A6
The simultaneous turn of tour onboard cubes gives algorithm (A37).
[(F*2)C'r - (F*2)(Cr*2)] U' [(Cr*2)(F*2) - Cr(F*2)] U........A37
The same result gives process A38.
(UCr)*4 - (U*2) - (UCr)*4 - (U*2).......A38
To moving three angular cubes with a turn of two of them apply described for the sixth stage of assembly algorithm A7.
R'F' L'F - RF' LF...........A7
F'L' FR' - F'L FR...........A' 7
Moving of three angular cubes with a turn of all of three gives 22-rotations, but it is possible to manage it, using algorithm A7.
Paired moving of angular cubes is cross-wise made by process color of a side does not vary, that is cubes do not overturn.
[ (Cr*2) - U - (Cr*2) (U*2) ]*2..........A39
The parallel exchange of angular cubes gives algorithm A40
( R'D F'(D*2) - FD' R(U*2) )*2........A40

As a result of some operations the central cubes leave from the place. The cube changes orientation. But, as is known, color of a side can be defined on color of the central cube. That in the end of a problem rientation of all cube Was same, as well as in the beginning, operations of turn of all cube entered Of, Or, Ou and item. Each such operation is considered one course.